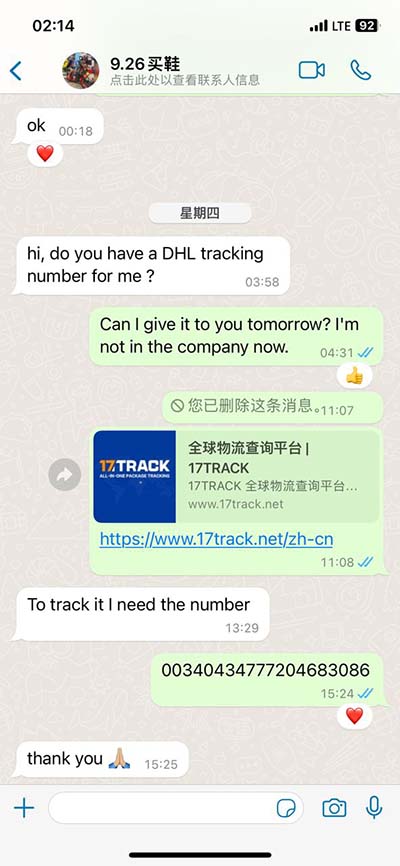
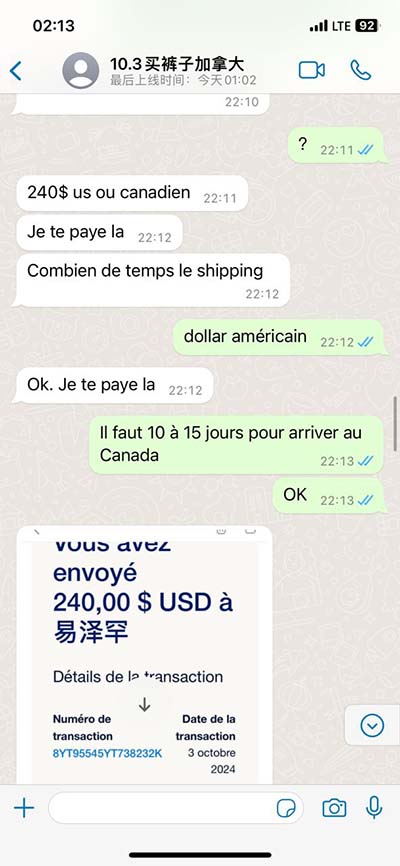
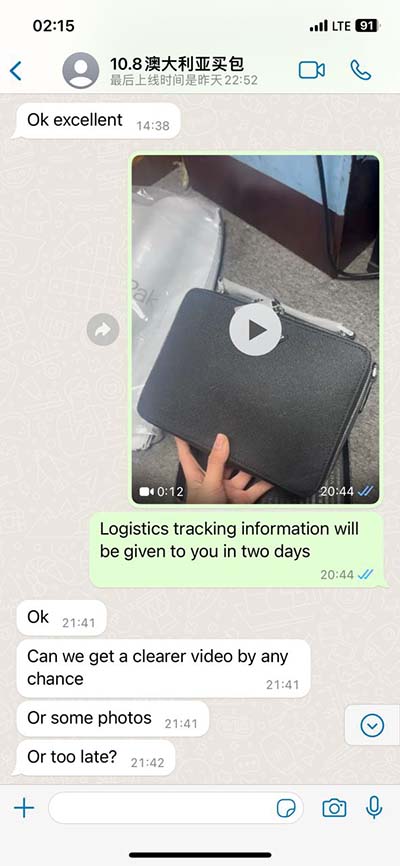
asin omega t At a fixed position x the displacement y varies as a function of time as y = Asin (ωt) = Asin [ (2π/T)t] with a convenient choice of origin. For the transverse harmonic wave y (x,t) = Asin (kx - ωt + φ) we may write. y (x,t) = Asin [ (2π/λ)x . Hero Stats. Max Avg Total Stats at Lvl 40 158. HP 41 Rank: 308 / 1016. ATK 34 Rank: 681 / 1016. SPD 35 Rank: 448 / 1016. DEF 27 Rank: 549 / 1016. RES 21 Rank: 815 / 1016.
0 · y a sin omega tkx
1 · omega t youtube
2 · omega t unit circle
3 · omega t sine vs sine
4 · omega t sine
5 · omega t kx sin
6 · omega t kx
7 · asin kx cos t
Andres Felipé Valencia Barrientos[1] (born: August 6, 1995 (1995-08-06) [age 28])[2] better known online as Yung Filly is a Colombian-British[3] YouTuber and musician. He is known for collabing with Chunkz and Harry Pinero, he also appear in .
A more general way of writing the equation for the motion would be: x(t)=A \sin(\omega t + \phi) where \phi is the phase constant. You find the value of \phi simply by looking to see what . What is correct wave equation: $y=A \sin(\omega t-kx)$ or $y=A\sin(kx-\omega t)$? How are these wave equations used in the positive .
Understanding Angular velocity, Omega t (wt), Sine, Unit Circle and Phase difference - YouTube. Electronics4Engineers - James Cleves. 1.03K subscribers. Subscribed. 88. 4.6K views 3 years.At a fixed position x the displacement y varies as a function of time as y = Asin (ωt) = Asin [ (2π/T)t] with a convenient choice of origin. For the transverse harmonic wave y (x,t) = Asin (kx - ωt + φ) we may write. y (x,t) = Asin [ (2π/λ)x .The wave function modeling a sinusoidal wave, allowing for an initial phase shift ϕ, is. y(x, t) = Asin(kx ∓ ωt + ϕ) The value. (kx ∓ ωt + ϕ) is known as the phase of the wave, where ϕ is the initial phase of the wave function. Whether the .A sine wave is a function of the time \(t\): \[y(t)=A\sin(\omega t - \phi)\] The phase of a sine wave, \(\phi\), is the displacement of the wave when \(t=0\). The angular frequency of a sine wave, \(\omega\), has the unit rad/s. The frequency of a .
y a sin omega tkx
Taking the first and second time derivative of x(t) and substituting them into the force equation shows that x(t) = Asin(\(\omega t + \phi\)) is a solution as long as the amplitude is equal to \[A = \frac{F_{0}}{\sqrt{m^{2} (\omega^{2} - .
hermes spich
You did get i\sin(\omega t) in your solution because that is the result of your calculation and this result is correct. There is no need to want \sin(\omega t) in the solution with your . More Items. Share. Copy. Copied to clipboard. Examples. Quadratic equation { x } ^ { 2 } - 4 x - 5 = 0.Here are some assumptions: An external AC voltage source will be driven by the function \(V ={ V }_{ o }\sin { (\omega t) } \), where \(V\) is the instantaneous potential difference in the circuit, \({ V }_{ o }\) is the maximum value in the .
When you pluck a guitar string, the resulting sound has a steady tone and lasts a long time (Figure \(\PageIndex{1}\)). The string vibrates around an equilibrium position, and one oscillation is completed when the string starts from the initial . Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this siteHint: In this question one has to know to compare the given equation $\left( {\sin \omega t - \cos \omega t} \right)$ with the general equation of Simple harmonic motion. If the equation matches with the general equation of Simple Harmonic Motion then the given equation is of SHM otherwise it is not. Complete step by step solution:
Tour Start here for a quick overview of the site Help Center Detailed answers to any questions you might have Meta Discuss the workings and policies of this site The product $\omega t$ is a dimensionless quantity and the same is true for $\sin{\omega t}$.If they are dimensionless, then they are identical between the rest and relativistic frames because there is no dimensions of time or length to dilate or contract.y = Asinω t + ϕo is the time – displacement equation of an SHM. At t = 0, the displacement of the particle is Y =A2 and it is moving along negative x direction. Then, the initial phase angle ϕo will be. 00:00 Contents00:25 Y=A Sin(wt) - describing Sine Wave features00:45 The unit circle01:11 Sine values for radians and degrees in a right-angled triangle02:38.
Our next important topic is something we've already run into a few times: oscillatory motion, which also goes by the name simple harmonic motion.This sort of motion is given by the solution of the simple harmonic oscillator (SHO) equation, \[ \begin{aligned} m\ddot{x} = -kx \end{aligned} \]Energy in Simple Harmonic Motion; Harmonic Oscillator Subject to an External, Constant Force; A particularly important kind of oscillatory motion is called simple harmonic motion. This is what happens when the restoring force is linear in the displacement from the equilibrium position: that is to say, in one dimension, if \(x_0\) is the equilibrium position, the restoring force has the formDet vil sige, \( \sin ( \omega t ) \) vil nå at løbe en halv periode igennem på samme tid som \( \sin(t) \) når 1 periode igennem, altså er frekvensen for \( \sin ( \omega t ) \) halvt så stor som for \( \sin (t) \). I figuren nedenfor er der skitseret 3 grafer med forskellige værdier for \( \omega \).
$$ x(t) = A_1 \cos \omega t + A_2 \sin \omega t $$ Note there are two constants of integration that correspond to the equation being a second order differential equation. More physically, the velocity is given by $$ v(t) = - \omega A_1 \sin \omega t .Pulses. A pulse can be described as wave consisting of a single disturbance that moves through the medium with a constant amplitude. The pulse moves as a pattern that maintains its shape as it propagates with a constant wave speed. Because the wave speed is constant, the distance the pulse moves in a time Δt is equal to Δx = vΔt (Figure \(\PageIndex{1}\)).
So you found that the pair $(\vec A,\vec B)$ is a "rotation" of the pair $(\vec a,\vec b)$ (an application of a rotation matrix to the pair as 2-column matrix). You can rotate that back, $$ \vec a=\vec A\cos\phi+\vec B\sin\phi\ \vec b=-\vec A\sin\phi+\vec B\cos\phi $$ Now the condition for orthogonality leads to an equation for $\phi$, $$ 0=\langle\vec A,\vec . I am trying to find the Laplace transform of $\sin(\omega t + \phi)$.My work is as follows: $$\begin{align} \mathcal{L} \{ \sin(\omega t + \phi) \} &= \int_0^\infty . The simple harmonic oscillator is solved by the differential equation $$ \frac{d^2x}{dt^2} = -kx $$ This differential equation is second order, so it needs two initial conditions. Categorise the following function oftime `: sin omega t + cos omega t ` as (a) Simple harmonic motion (b) Periodic but not simple harmonic. Also, give the pe.
The other wave of representing a wave is to draw a wave profile which is essentially an instantaneous photograph of the wave. Both the graphs illustrate quite clearly that the waves are travelling in the positive x-direction. As a side note, one thing that students sometimes forget when working this problem is that waves are inverted when reflected from a fixed point (i.e. a very stiff interface), so the the starting form should be something like \begin{align} Y(x,t) &= &y_+(x,t) &\color{red}{-} y_-(x,t) \ &= &A \sin( k x - \omega t) &- A \sin( k x + \omega t) \;. \end{align} The handling of that minus .
Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more. Stack Exchange Network. Stack Exchange network consists of 183 Q&A communities including Stack Overflow, the largest, most trusted online community for developers to learn, share their knowledge, and build their careers.. Visit Stack Exchange A point performs simple harmonic oscillation of period T and the equation of motion is given by `x = a sin (omega t + (pi)/(6))`. After the elapse of . asked Dec 19, 2019 in Physics by EashtaBasu (97.5k points) class-12; neet +2 votes. 1 answer. A particle performs simple harmonic motion with amplitude A. Take \[ 0.5 x'' + 8 x = 10 \cos (\pi t), \quad x(0) = 0, \quad x' (0) = 0 \nonumber \] Let us compute. First we read off the parameters: \( \omega = \pi, \omega_0 .
The motion of a particle is given by x = A sin ωt + B cos ωt.The motion of the particle is (a) not simple harmonic (b) simple harmonic with amplitude A + B (c) simple harmonic with amplitude (A + B)/2 (d) simple harmonic with amplitude A 2 + B 2.Solve your math problems using our free math solver with step-by-step solutions. Our math solver supports basic math, pre-algebra, algebra, trigonometry, calculus and more.
You did get i\sin(\omega t) in your solution because that is the result of your calculation and this result is correct. There is no need to want \sin(\omega t) in the solution with your .

I'm personally fond of reclassing base classes at level 10 if I do reclass a base class, after they learn their skills, then (assuming I'm promoting in that other base class) I promote them at 10. You could delay the levels a .
asin omega t|omega t sine vs sine